Primer: Genome Assembly
Overview
Genome assembly refers to the process of accurately constructing a contiguous representation of nucleotides based on a collection of smaller sequence fragments. Currently, scientists primarily employ graph-based approaches to represent the relationships between DNA fragments obtained from high-throughput genome sequencing, increasing the reproducibility and scalability of de novo genome assembly. Although these approaches contribute to resolving repetitive regions of DNA without relying on a reference genome, the overall accuracy of the assembly is often limited by genome size, sequencing errors, and algorithmic complexity. As incorrectly reported sequences may subsequently affect downstream analysis, increasing the performance of genome assembly will enhance our overall understanding of genetic diseases across various species and provide greater sensitivity for detecting indels and structural variation in the genome.
In this module, we will provide an overview of graph data structures and their common representations. Furthermore, we will outline the primary algorithms for genome assembly, highlighting their characteristics, advantages, and disadvantages on various types of sequences.
What is a Graph?
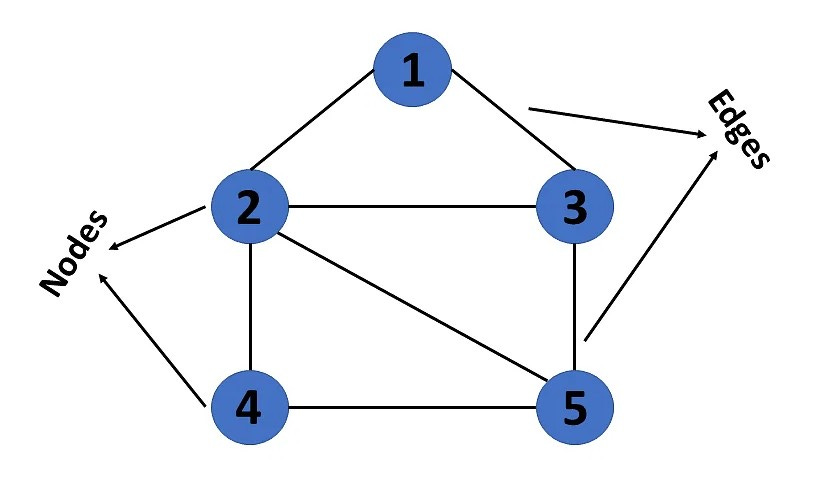
A graph is a non-linear data structure that represents the relationship between multiple entities. In mathematical notation, graphs are denoted as G(V, E), where V represents a pair of vertices/nodes and E represents a pair of edges/arcs. In genome assembly, each sequencing read is represented by a vertex and the degree of overlap between two reads is represented by a directed edge.
Types of Graphs
As depicted in the following graphic, graphs may be directed or undirected, cyclic or acyclic, weighted or unweighted, and dense or sparse.

In a directed graph, the edges travel only in one direction. In an undirected graph, the edges travel in both directions.
In a cyclic graph, there is at least one cycle present, where a cycle is a path in which the beginning and ending nodes are identical. In an acyclic graph, there are no cycles present.
In a weighted graph, each edge is associated with a cost or distance. In an unweighted graph, the edges are not associated with a cost or distance.
In a dense graph, the number of edges is similar to the maximum number of edges. In a sparse graph, the number of edges is similar to the minimum number of edges.
Graph Representations

Adjacency Matrix
An adjacency matrix is a two-dimensional array of size V x V, where V represents the number of vertices in the graph. If an edge exists between vertices i and j, then the value in the corresponding cell is 1; otherwise the value is 0. In the context of genome assembly, each contig corresponds to a vertex in the graph.
The adjacency matrix representation is preferred when representing dense graphs. However, this representation becomes inefficient when adding or removing nodes, as this operation has an algorithmic runtime complexity of O(N2).
Adjacency List
An adjacency list is a one-dimensional array of linked lists. In each linked list, the first node represents the vertex and each element in the linked list corresponds to a neighboring vertex that shares an edge.
The adjacency list representation is preferred when representing sparse graphs. Compared to the adjacency matrix representation, the adjacency list is both memory-efficient and space-efficient, as it only stores the values for the edges in the graph.
Approaches for Genome Assembly
Greedy Approach
The greedy approach for de novo genome assembly selects the optimal extension or merging of sequence fragments at each step without reconsidering or modifying prior decisions in the subsequent iterations of the algorithm. Although this approach to genome assembly is fairly intuitive, the algorithm is often complicated by unresolvable repeats and sequencing errors. Specifically, the locally optimal decisions made at each step may not result in a globally optimal solution, increasing the likelihood of inaccurate assemblies for repetitive regions of the genome.
Greedy Assembly Algorithm
Randomly select a sequence read.
Identify the read with the greatest number of overlapping nucleotides.
Align the reads.
Repeat steps 1-3.
When the sequence is unable to extend further, it becomes the contig. At this point, return to step 1 and repeat with a random read until the entire sequence is complete.
Overlap-Layout-Consensus (OLC) Approach
The OLC approach for de novo genome assembly is appropriate for long-read sequencing data and derives a consensus sequence based on the overlaps between reads. This approach handles repeats by removing cycles in the graph, excluding them from the final assembly. However, this approach is inefficient when assembling larger genomes. Furthermore, the presence of unresolvable repeats will often fragment the assembly into contigs.
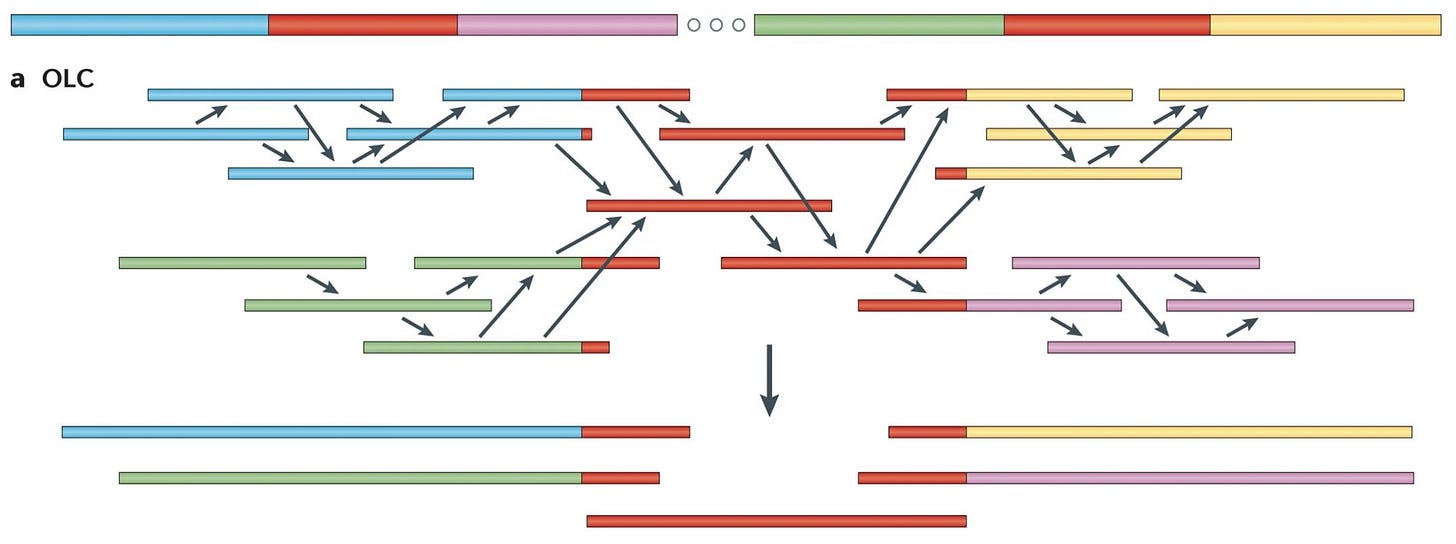
OLC Assembly Algorithm
Overlap: Construct the overlap graph based on the entire set of k-mers, a sequence of length k.
Layout: Remove inferable edges by combining segments of the overlap graph into contigs.
Consensus: Select the most likely nucleotide sequence for each contig, the overlap between two reads.
De Bruijn Graph Assembly
The De Bruijn graph approach for de novo genome assembly is appropriate for short-read sequencing data and reconstructs the sequence based on the overlaps in a set of k-mers. Although this approach maximizes the efficiency of computation and data storage, it requires a set of accurate sequencing reads and excludes repeats from the assembly, resulting in a higher degree of information loss.
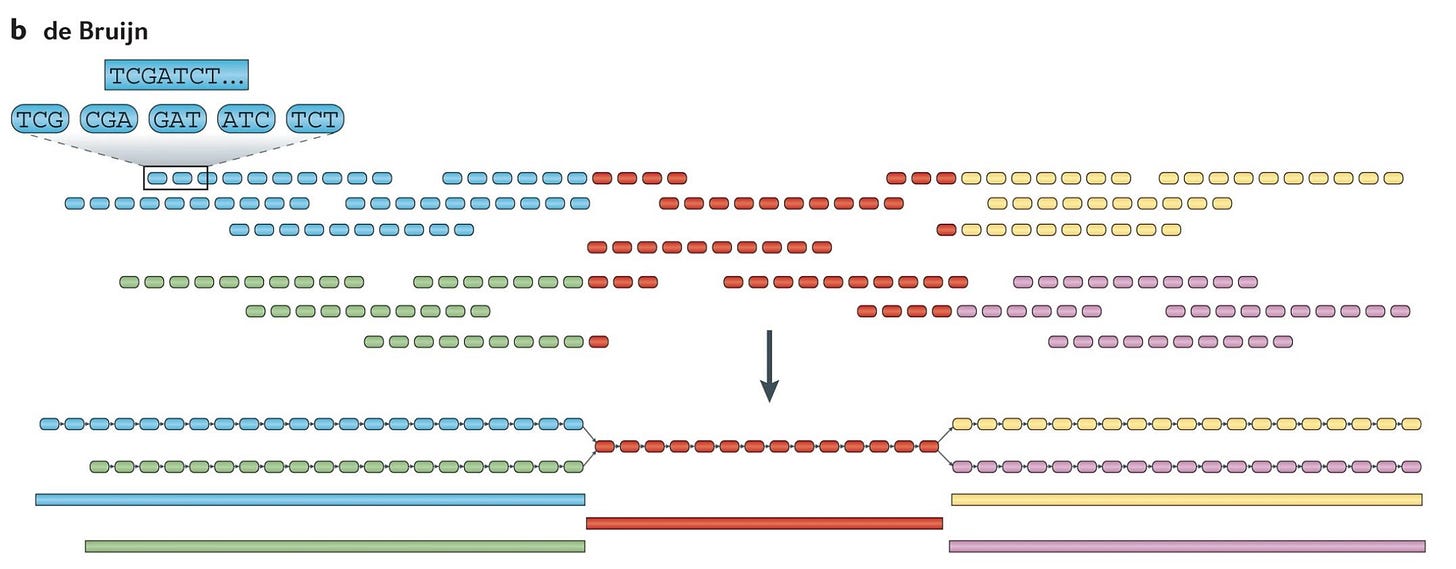
De Bruijn Graph Algorithm
Assumptions: All sequencing reads are accurate and each k-mer appears only once.
Fragment each read into k-mers.
Identify the prefix and suffix of all k-mers.
Generate edges based on the overlap between k-mers.
The final sequence is determined by the Eulerian cycle, a path with the same starting and ending vertex that visits every edge only once.
References
[1] Chaisson, M., Wilson, R., & Eichler, E. Genetic variation and the de novo assembly of human genomes. Nat Rev Genet 16, 627–640 (2015). https://doi.org/10.1038/nrg3933



